CALCULO DIFERENCIAL
Definición de Derivada
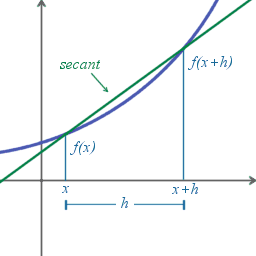
Las derivadas se definen tomando el límite de la pendiente de las rectas secantes conforme se van aproximando a la recta tangente.
Es difícil hallar directamente la pendiente de la recta tangente de una función porque sólo conocemos un punto de ésta, el punto donde ha de ser tangente a la función. Por ello, aproximaremos la recta tangente por rectas secantes. Cuando tomemos el límite de las pendientes de las secantes próximas, obtendremos la pendiente de la recta tangente.
 Para obtener estas pendientes, tomemos un número arbitrariamente pequeño que llamaremos h. h representa una pequeña variación en x, y puede ser tanto positivo como negativo. La pendiente de la recta entre los puntos ( x, f(x)) y (x + h, f(x + h))es
Para obtener estas pendientes, tomemos un número arbitrariamente pequeño que llamaremos h. h representa una pequeña variación en x, y puede ser tanto positivo como negativo. La pendiente de la recta entre los puntos ( x, f(x)) y (x + h, f(x + h))es
Esta expresión es un Cociente Diferencial de Newton. La derivada de f en x es el límite del valor del cociente diferencial conforme las líneas secantes se acercan más a la tangente:
Si la derivada de f existe en cada punto x, podemos definir la derivada de f como la función cuyo valor en el punto x es la derivada de f en x.
 Puesto que la inmediata sustitución de h por 0 da como resultado una división por cero, calcular la derivada directamente puede ser poco intuitivo. Una técnica es simplificar el numerador de modo que la h del denominador pueda ser cancelada. Esto resulta muy sencillo con funciones polinómicas, pero para la mayoría de las funciones resulta demasiado complicado. Afortunadamente, hay reglas generales que facilitan la diferenciación de la mayoría de las funciones descritas.
Puesto que la inmediata sustitución de h por 0 da como resultado una división por cero, calcular la derivada directamente puede ser poco intuitivo. Una técnica es simplificar el numerador de modo que la h del denominador pueda ser cancelada. Esto resulta muy sencillo con funciones polinómicas, pero para la mayoría de las funciones resulta demasiado complicado. Afortunadamente, hay reglas generales que facilitan la diferenciación de la mayoría de las funciones descritas.Notaciones para la diferenciación
 para la primera derivada,
para la primera derivada, para la segunda derivada,
para la segunda derivada, para la tercera derivada, y luego de forma general,
para la tercera derivada, y luego de forma general, para la n-ésima derivada (donde normalmente se da que n > 3).
para la n-ésima derivada (donde normalmente se da que n > 3).

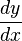
 o
o 


 .
.

 ,
,
La derivada de una función puede a su vez ser diferenciable, hablándose entonces de segunda derivada de la función como la derivada de la derivada de ésta. Análogamente, la derivada de la segunda derivada recibe el nombre de tercera derivada, y así sucesivamente.
A partir de la segunda derivada: f " (a) hasta la enésima derivada:  reciben el nombre de Derivada de Orden Superior.
reciben el nombre de Derivada de Orden Superior.
 reciben el nombre de Derivada de Orden Superior.
reciben el nombre de Derivada de Orden Superior.
La notación más simple para la diferenciación que se utiliza en la actualidad se debe a Lagrange y utiliza un apóstrofo o comilla: ′. De esta manera se expresan las derivadas de la función f(x) en el punto  , se escribe:
, se escribe:
 , se escribe:
, se escribe: es la derivada de
es la derivada de 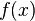 , se escribe
, se escribe 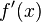 . De forma similar, para la segunda derivada de
. De forma similar, para la segunda derivada de  se escribe
se escribe  , y así sucesivamente.
, y así sucesivamente.La otra notación común para la diferenciación se debe a Leibniz. Para la función cuyo valor en
 es la derivada de
es la derivada de  en
en  , se escribe:
, se escribe:La notación de Leibniz es tan versátil que permite especificar la variable que se utilizará para la diferenciación (en el denominador). Esto es específicamente relevante para la diferenciación parcial. Y también hace más fácil de recordar la regla de la cadena, debido a que los términos "d" se cancelan simbólicamente:
La notación de Newton para la diferenciación consiste en poner un punto sobre el nombre de la función:
La notación de Newton se utiliza principalmente en la mecánica, normalmente para las derivadas con respecto al tiempo tales como la velocidad y la aceleración y en la teoría de ecuaciones diferenciales ordinarias. Normalmente sólo se utilizan para la primera y segunda derivadas.
Otra notación consiste en colocar una letra 'D' mayúscula para indicar la operación de diferenciación con un subíndice que indica la variable sobre la que se derivará:

